
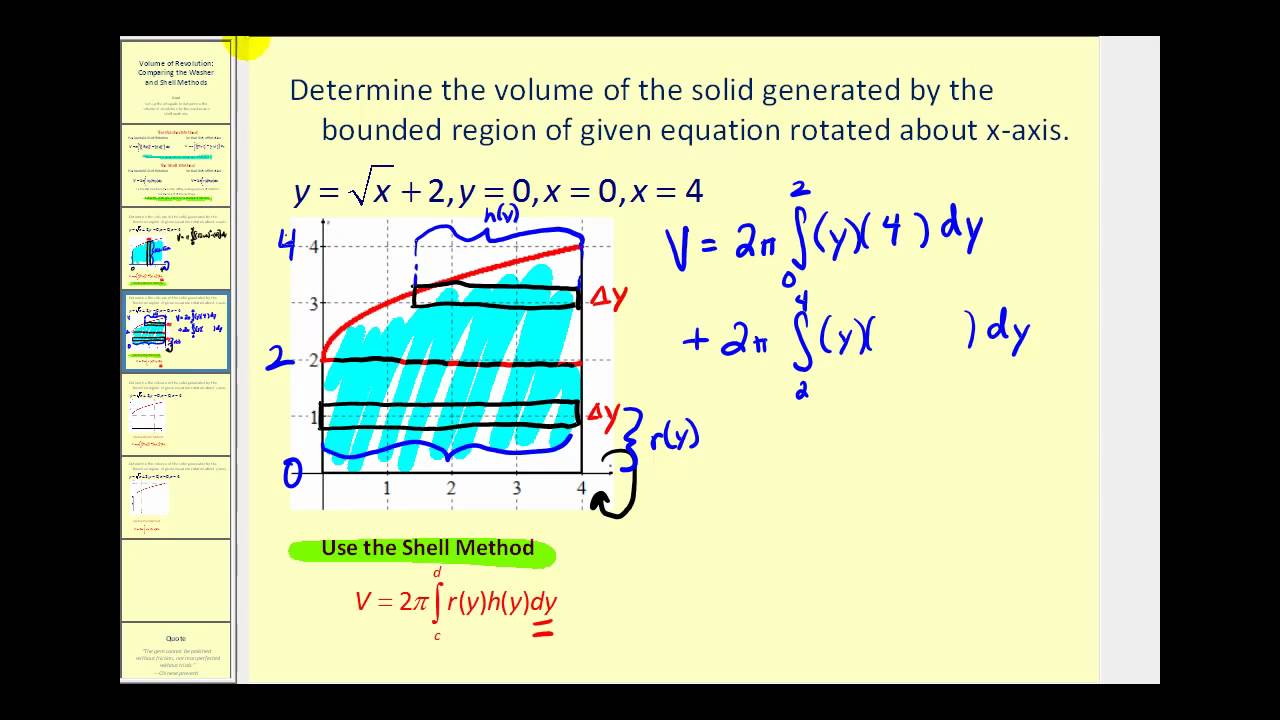
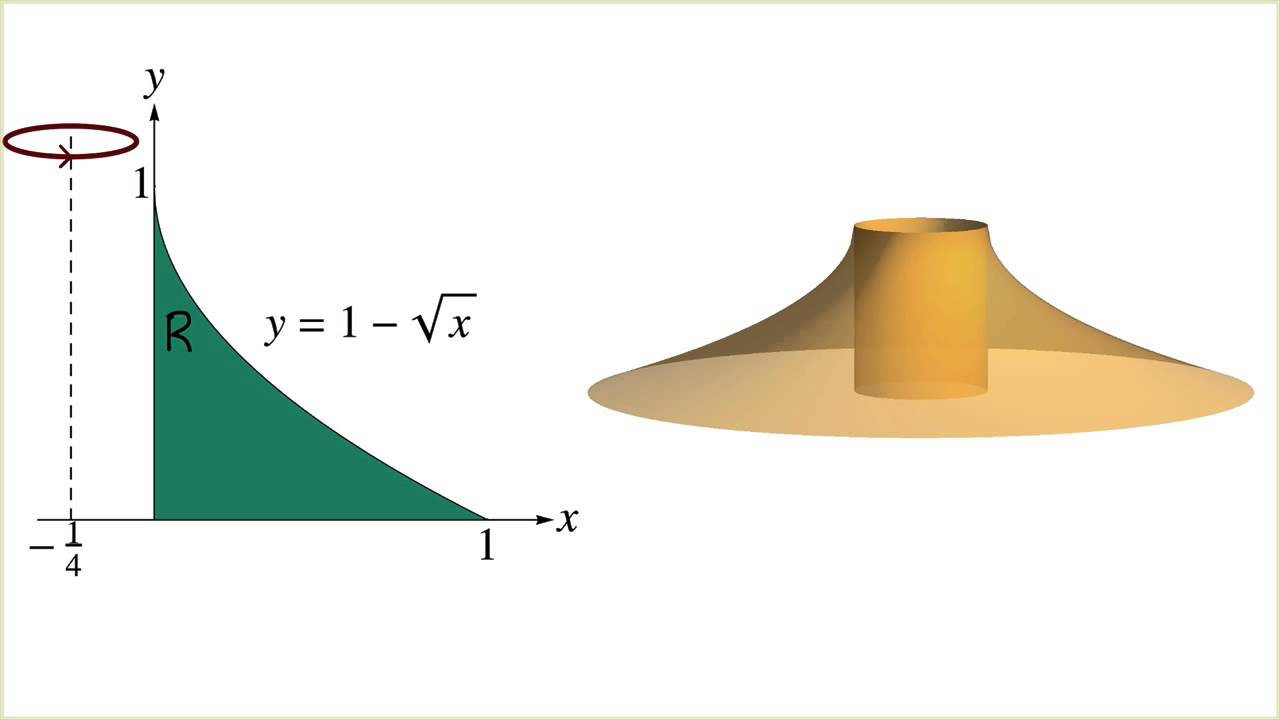
Suppose the region R is bounded by two curves, y = f(x) and y = g(x), where f(x) ≥ g(x) on. The height of the slab is the height of the original rectangle f(xk*) and its thickness is ∆x therefore, the volume of the kth shell is approximatelyħ Summing the volume of the n cylindrical shells given an approximation to the volume of the entire solid: As n increases and as ∆x approaches 0, we obtain the exact volume of the solid as a definite integral:ĩ Before doing examples, we generalize this method as we did for the disk method. The approximate length of the slab is the circumference of a circle with radius xk*, which is 2xk*. As it revolves about the y-axis, this rectangle sweeps out a thin cylindrical shell.ĥ When the kth cylindrical shell is unwrapped, it approximates a thin rectangle slab. Now observe the rectangle build on the kth subinterval with a height of f(xk*) and a width ∆x. When R is revolved about the y-axis, a solid is generated whose volume is computed with the slice-and-sum strategy.Ĥ We divide into the n subintervals of length ∆x = (b - a)/n, and identify an arbitrary point xk* on the kth subinterval, for k = 1,…,n. Cylindrical Shells Let R be a region bounded by the graph of f, the x-axis, and the lines x = a and x = b, where 0 ≤ a < b and f(x) ≥ 0 on.

For this reason, we extend our discussion of volume problems to the shell method, which, as in the disk/washer method, is used to compute the volume of solids of revolution. There are, however, some volume problems that are difficult to solve with this method. 2 One can solve a lot of challenging volume problems using the disk/washer method.


 0 kommentar(er)
0 kommentar(er)
